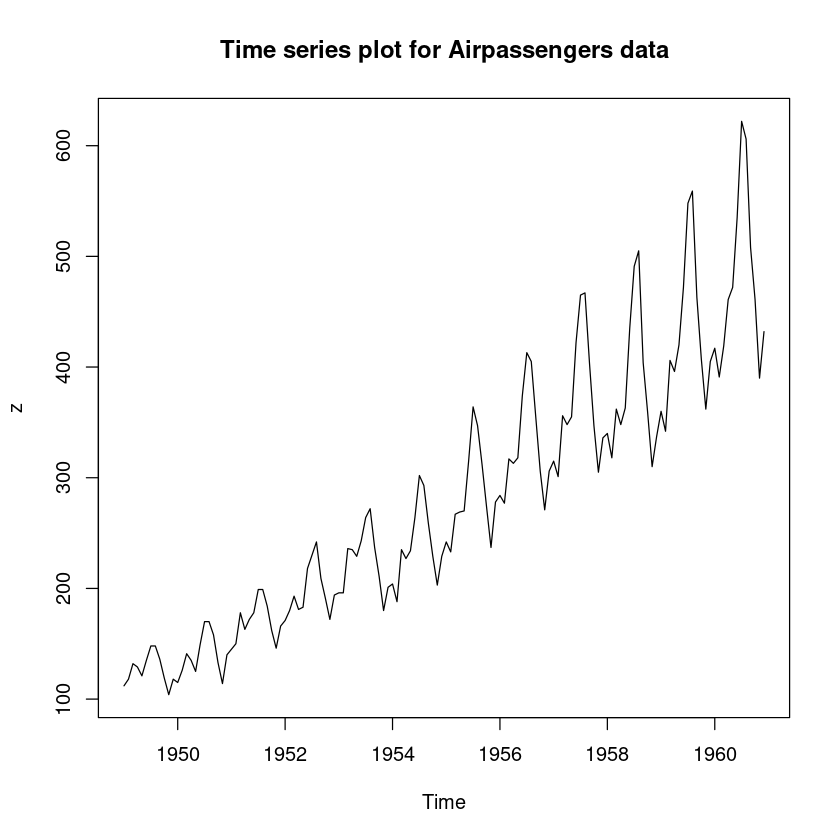
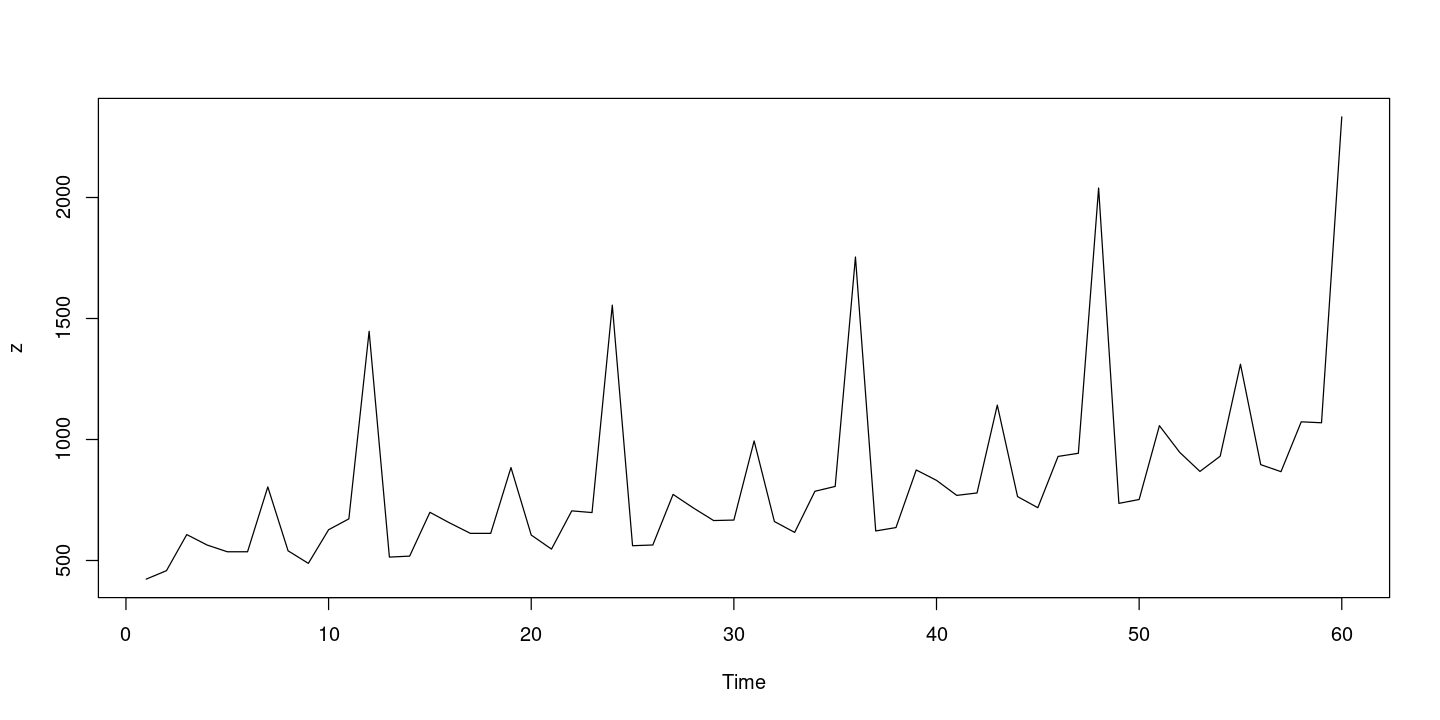
분산이 일정하지 않은 경우
A Time Series: 12 × 12
1949
112
118
132
129
121
135
148
148
136
119
104
118
1950
115
126
141
135
125
149
170
170
158
133
114
140
1951
145
150
178
163
172
178
199
199
184
162
146
166
1952
171
180
193
181
183
218
230
242
209
191
172
194
1953
196
196
236
235
229
243
264
272
237
211
180
201
1954
204
188
235
227
234
264
302
293
259
229
203
229
1955
242
233
267
269
270
315
364
347
312
274
237
278
1956
284
277
317
313
318
374
413
405
355
306
271
306
1957
315
301
356
348
355
422
465
467
404
347
305
336
1958
340
318
362
348
363
435
491
505
404
359
310
337
1959
360
342
406
396
420
472
548
559
463
407
362
405
1960
417
391
419
461
472
535
622
606
508
461
390
432
plot.ts (z, main = "Time series plot for Airpassengers data" )
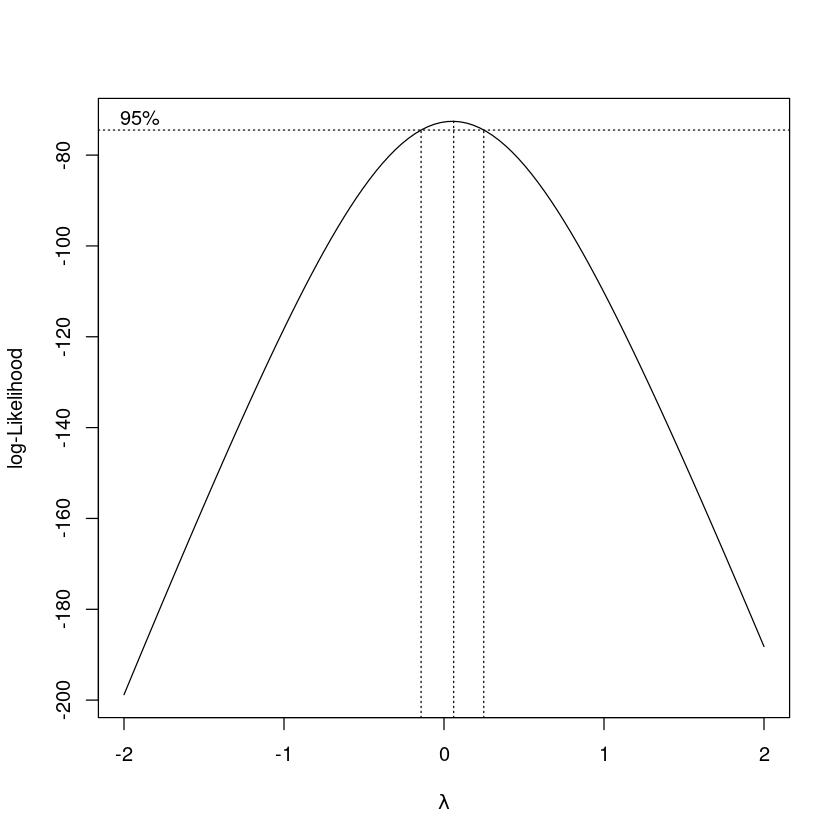
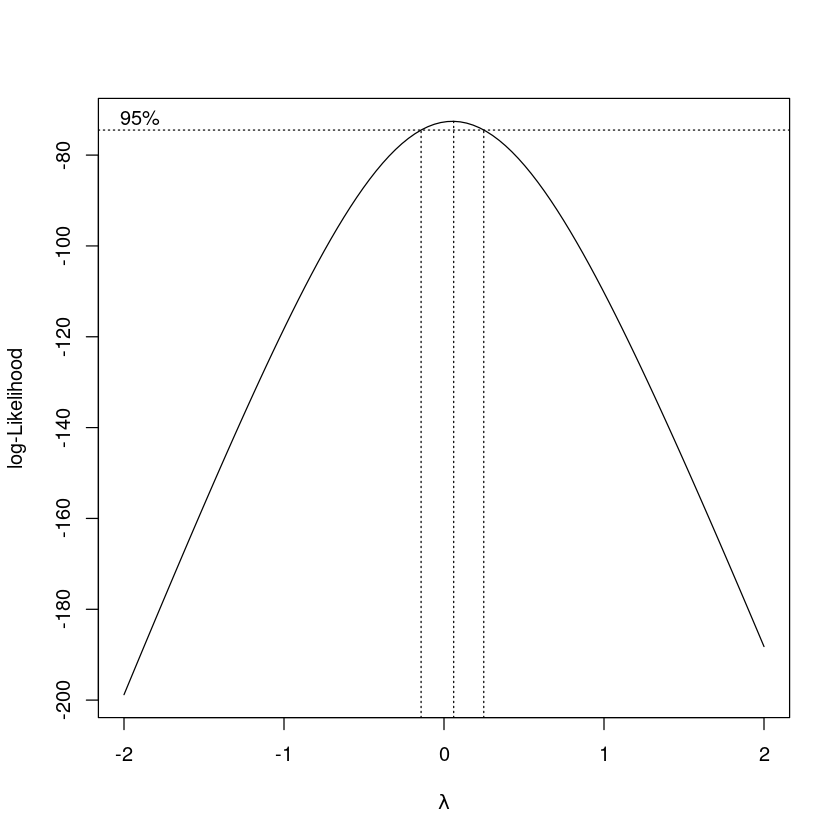
- Box-Cox transformation
\[f_\lambda(Z_t) = \begin{cases}
\dfrac{Z_t^\lambda-1}{\lambda}, & Z_t \geq 0, \lambda>0 \\
log(Z_t), & \lambda=0
\end{cases}\]
:: BoxCox.lambda (z, method= 'loglik' )
Registered S3 method overwritten by 'quantmod':
method from
as.zoo.data.frame zoo
0.2
:: BoxCox.lambda (z, method = "guerrero" )
-0.294715585559316
- ts객체가 들어가야함
:: BoxCox (z,lambda= forecast:: BoxCox.lambda (z, method= 'loglik' ))
A Time Series: 12 × 12
1949
7.847352
7.982144
8.276536
8.215632
8.047493
8.336343
8.583833
8.583833
8.356042
8.004073
7.658338
7.982144
1950
7.915451
8.153584
8.452835
8.336343
8.132639
8.602141
8.965606
8.965606
8.762630
8.296592
7.892911
8.433699
1951
8.528312
8.620350
9.094641
8.848653
8.998313
9.094641
9.412543
9.412543
9.188405
8.831619
8.546920
8.899258
1952
8.981998
9.126173
9.324566
9.141833
9.172949
9.677811
9.835957
9.987634
9.554566
9.294754
8.998313
9.339379
1953
9.368824
9.368824
9.912567
9.899908
9.823034
10.000000
10.250736
10.342064
9.925183
9.582316
9.126173
9.441397
1954
9.484251
9.249564
9.899908
9.797051
9.887205
10.250736
10.666479
10.571969
10.192525
9.823034
9.470023
9.823034
1955
9.987634
9.874459
10.285240
10.308071
10.319435
10.799092
11.262611
11.107788
10.768883
10.364560
9.925183
10.409160
1956
10.475107
10.398058
10.819103
10.778978
10.829071
11.351000
11.678616
11.613495
11.181384
10.707761
10.330766
10.707761
1957
10.799092
10.656090
11.190490
11.117061
11.181384
11.750682
12.078927
12.093594
11.605283
11.107788
10.697481
11.004343
1958
11.042269
10.829071
11.244701
11.117061
11.253666
11.852637
12.265784
12.363141
11.605283
11.217686
10.748614
11.013858
1959
11.226711
11.061098
11.621691
11.538992
11.734774
12.130041
12.649244
12.719537
12.064211
11.629871
11.244701
11.613495
1960
11.710799
11.497014
11.726798
12.049443
12.130041
12.564701
13.102063
13.007960
12.383721
12.049443
11.488567
11.829327
:: BoxCox (z,lambda= 'auto' )
A Time Series: 12 × 12
1949
2.548535
2.561426
2.588461
2.582990
2.567558
2.593773
2.615143
2.615143
2.595510
2.563492
2.529884
2.561426
1950
2.555089
2.577352
2.603953
2.593773
2.575434
2.616686
2.646282
2.646282
2.629992
2.590249
2.552929
2.602296
1951
2.610433
2.618215
2.656336
2.636968
2.648852
2.656336
2.680161
2.680161
2.663501
2.635595
2.612017
2.641022
1952
2.647572
2.658759
2.673698
2.659957
2.662328
2.699069
2.709945
2.720109
2.690390
2.671486
2.648852
2.674793
1953
2.676962
2.676962
2.715111
2.714262
2.709067
2.720927
2.737151
2.742897
2.715955
2.692360
2.658759
2.682259
1954
2.685357
2.668111
2.714262
2.707296
2.713408
2.737151
2.762643
2.756996
2.733443
2.709067
2.684331
2.709067
1955
2.720109
2.712549
2.739332
2.740768
2.741481
2.770427
2.796406
2.787934
2.768668
2.744300
2.715955
2.747066
1956
2.751119
2.746379
2.771588
2.769257
2.772164
2.801154
2.818211
2.814887
2.791987
2.765084
2.742191
2.765084
1957
2.770427
2.762027
2.792485
2.788447
2.791987
2.821853
2.837961
2.838662
2.814466
2.787934
2.764478
2.782161
1958
2.784288
2.772164
2.795437
2.788447
2.795922
2.826939
2.846793
2.851301
2.814466
2.793969
2.767483
2.782696
1959
2.794460
2.785340
2.815307
2.811044
2.821052
2.840400
2.864196
2.867286
2.837255
2.815726
2.795437
2.814887
1960
2.819842
2.808860
2.820650
2.836545
2.840400
2.860440
2.883580
2.879651
2.852247
2.836545
2.808419
2.825783
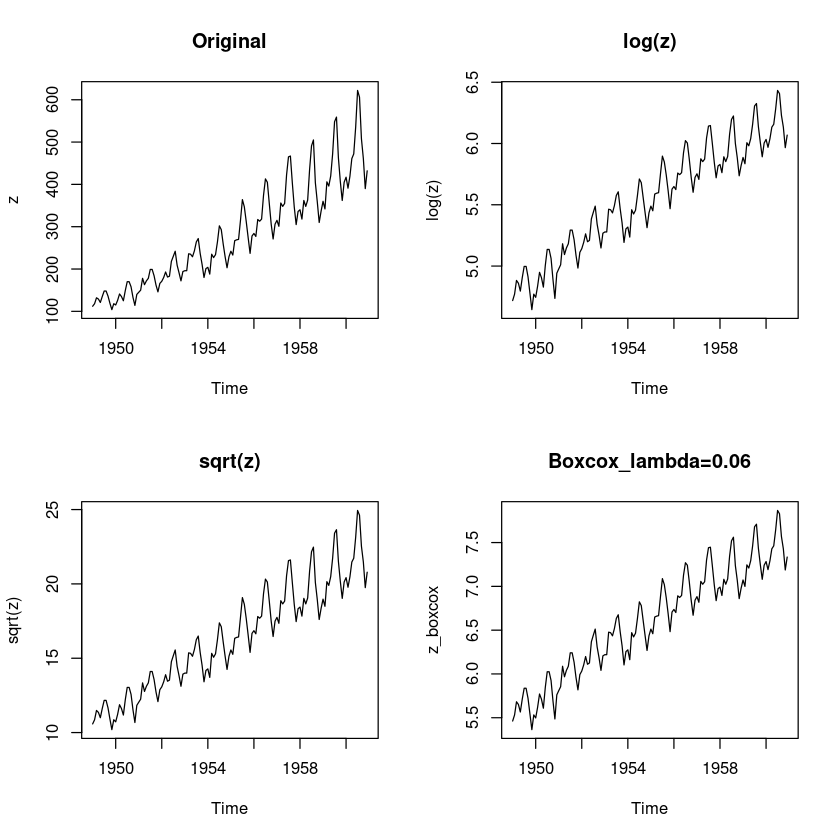
- linear model이 들어가야함
<- forecast:: BoxCox (z, lambda= bc$ x[which.max (bc$ y)])
par (mfrow= c (2 ,2 ))plot.ts (z, main = "Original" )plot.ts (log (z), main = "log(z)" )plot.ts (sqrt (z),, main = "sqrt(z)" )plot.ts (z_boxcox, main = "Boxcox_lambda=0.06" )graphics.off ()
확률적 추세 제거
- 확률보행과정의 정상화
\(Z_t = Z_{t−1} + ϵ_t, ϵ_t ∼ WN(0, σ^2)\) - AR(1) with \(ϕ = 1\)
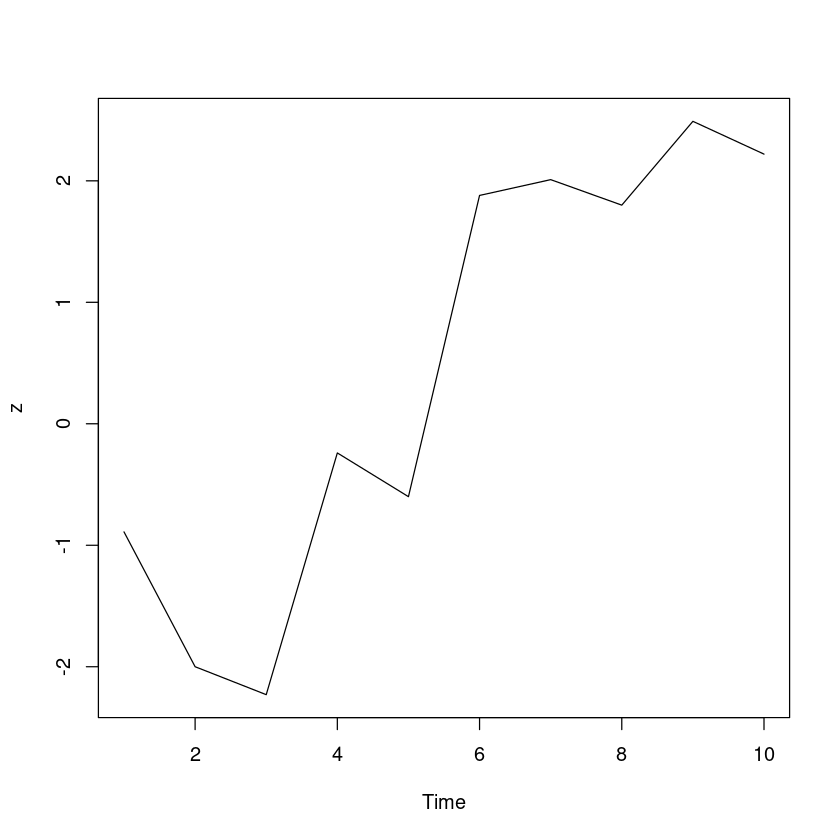
<- round (rnorm (10 ),2 )<- cumsum (e)plot.ts (z)
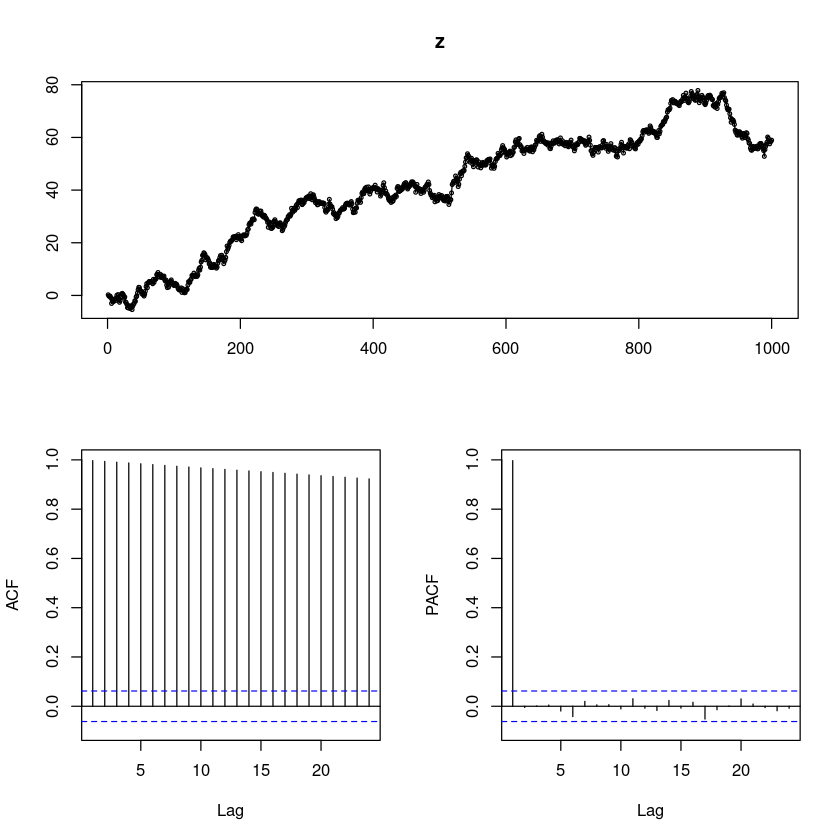
<- round (rnorm (1000 ),2 )<- cumsum (e):: tsdisplay (z, lag.max= 24 )
\(ΔZ_t = Z_t − Z_{t−1} = ϵ_t\)
차분한 확률보행과정의 시도표 및 ACF/PACF 그림
- diff:차분함수
예시
4: 7-3 : a[2]-a[1]
-5: 2-7 : a[3] - a[2]
7: 9-2 : a[4] - a[3]
-1: 2-3 : a[3] - a[1]
2: 9-7: a[4] - a[2]
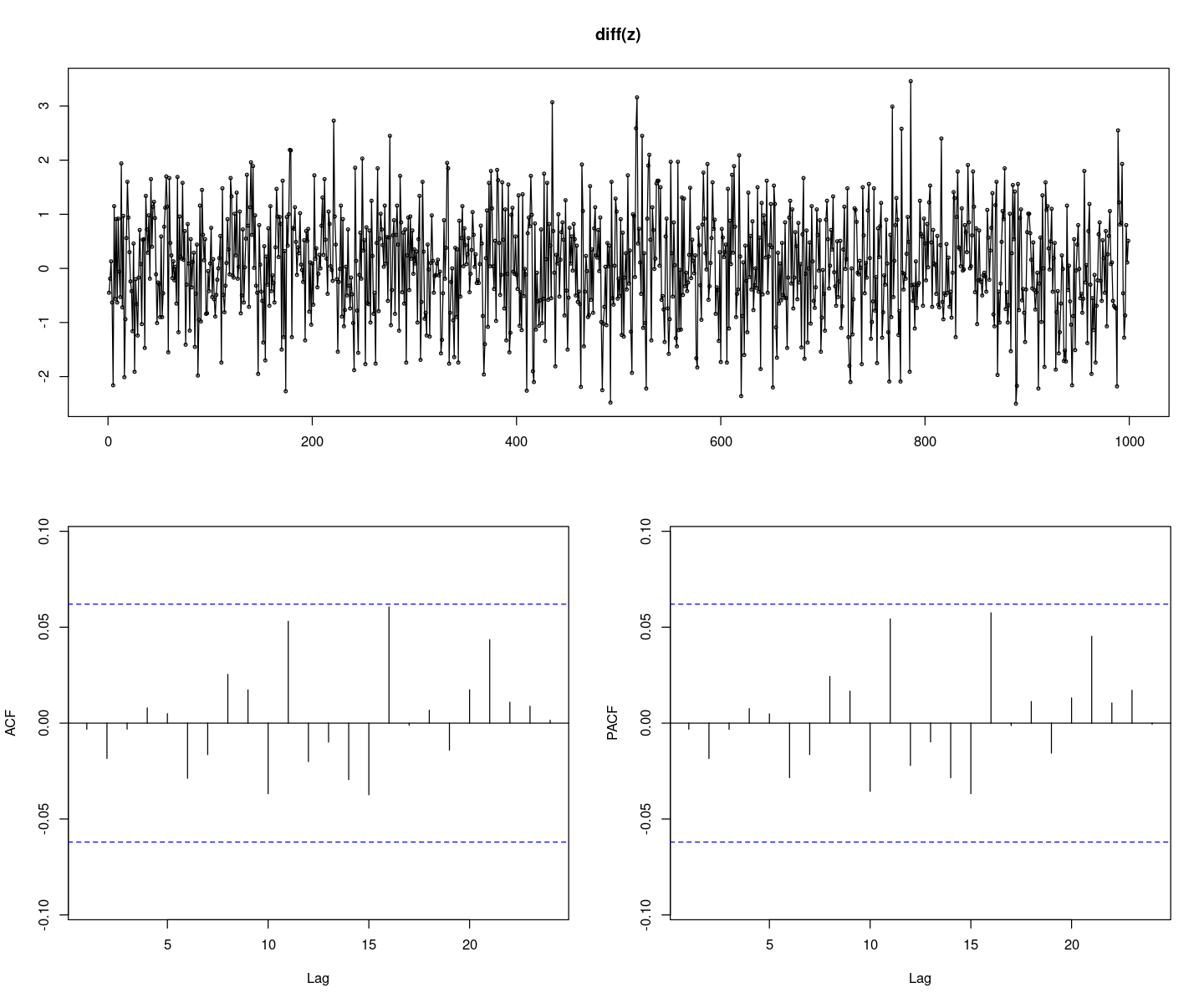
options (repr.plot.width = 12 , repr.plot.height = 10 ):: tsdisplay (diff (z), lag.max= 24 )
\(ΔZ_t ∼ WN = ARMA(0, 0) ⇒ Z_t ∼ ARIMA(0, 1, 0)\)
로그변환한 Airpassengers data 에 대한 확률적 추세 확인
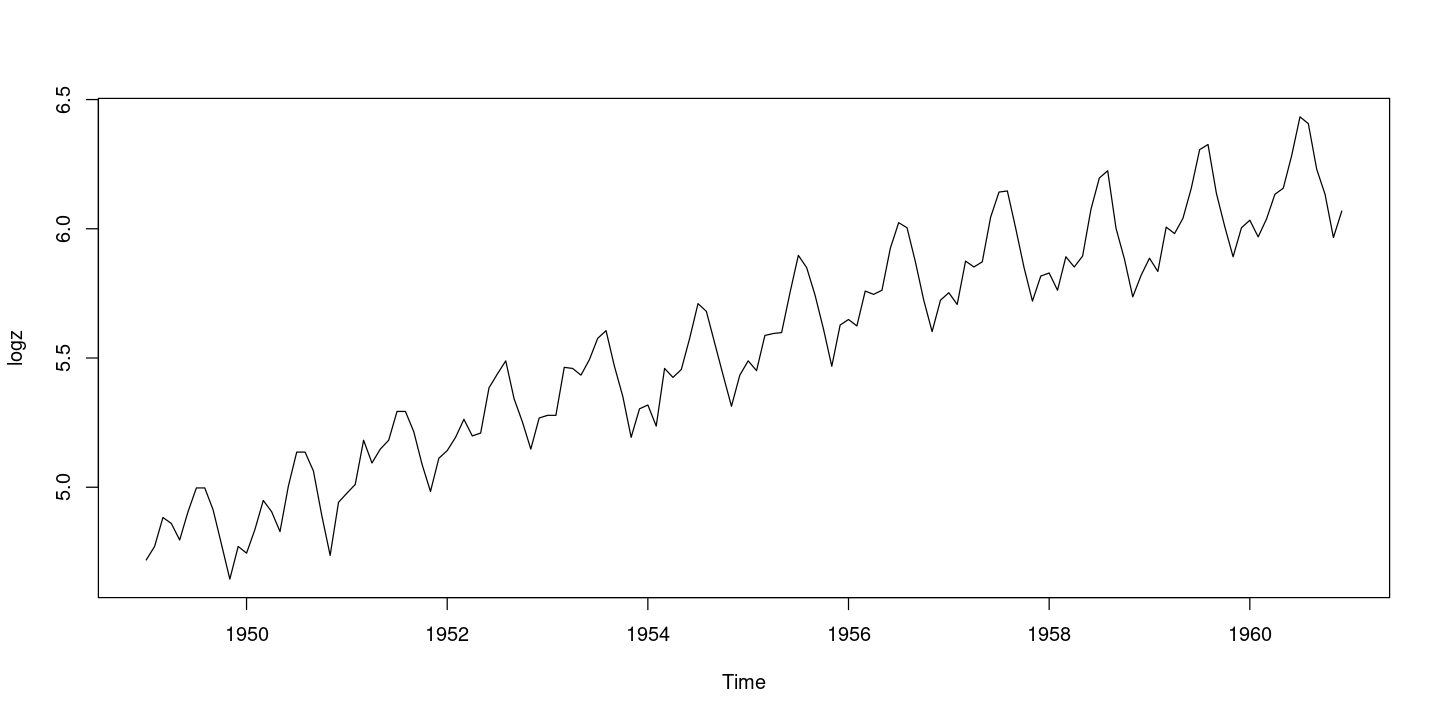
<- log (AirPassengers)options (repr.plot.width = 12 , repr.plot.height = 6 )plot.ts (logz)
추세가 있다. 결정적 추세로 해도 될거 같기도 하고…
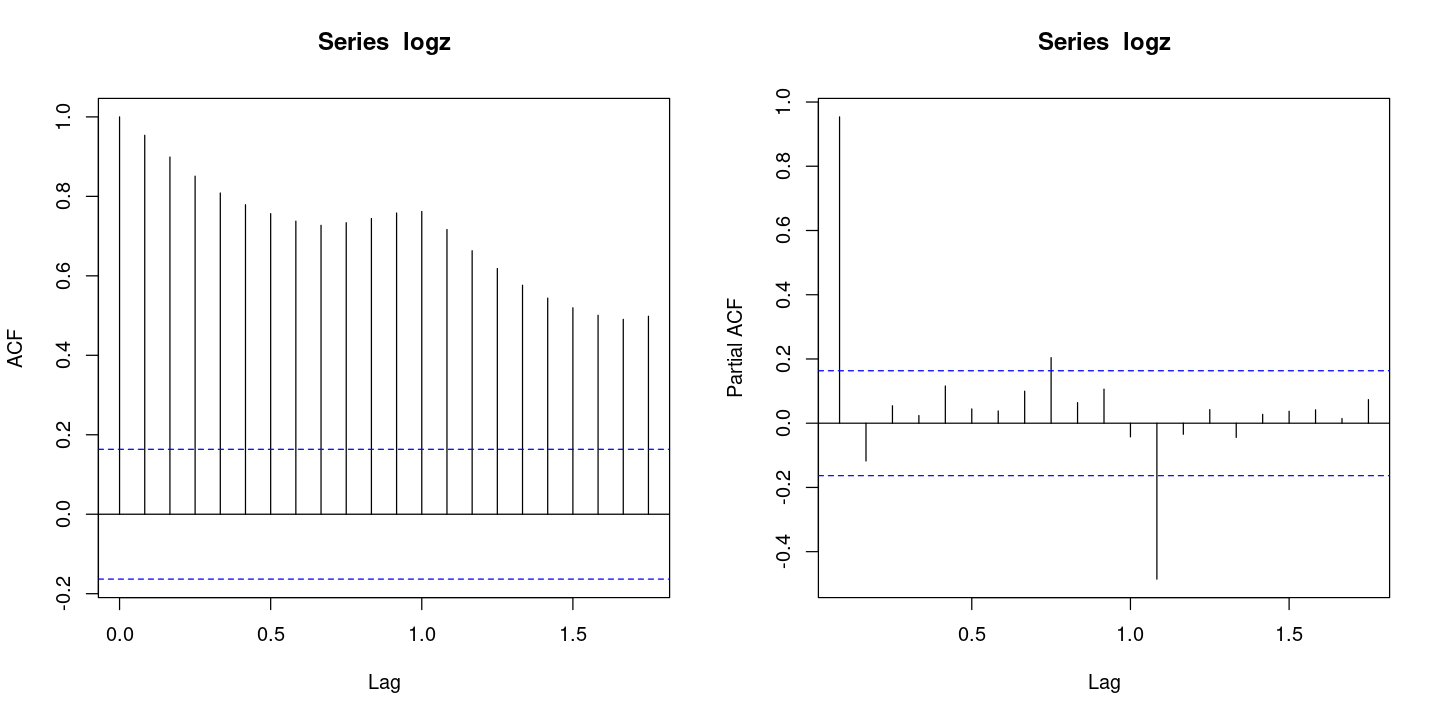
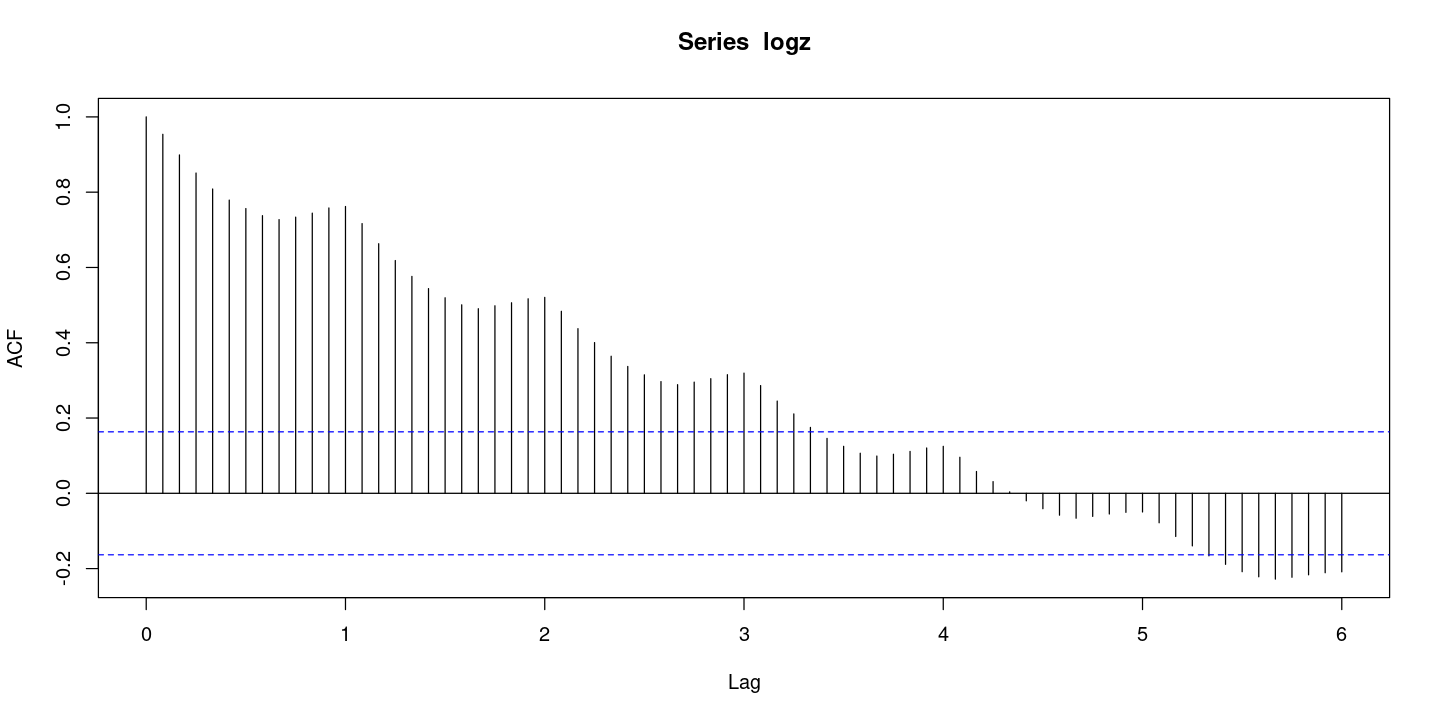
par (mfrow= c (1 ,2 ))acf (logz)pacf (logz)
계절성분 떄문에 acf그래프가 중간에 내려오다가 볼록 튀어 나온 것
차분을 진행한다.
\(ΔZ_t = (1 − B)Z_t = Z_t − Z_{t−1}\)
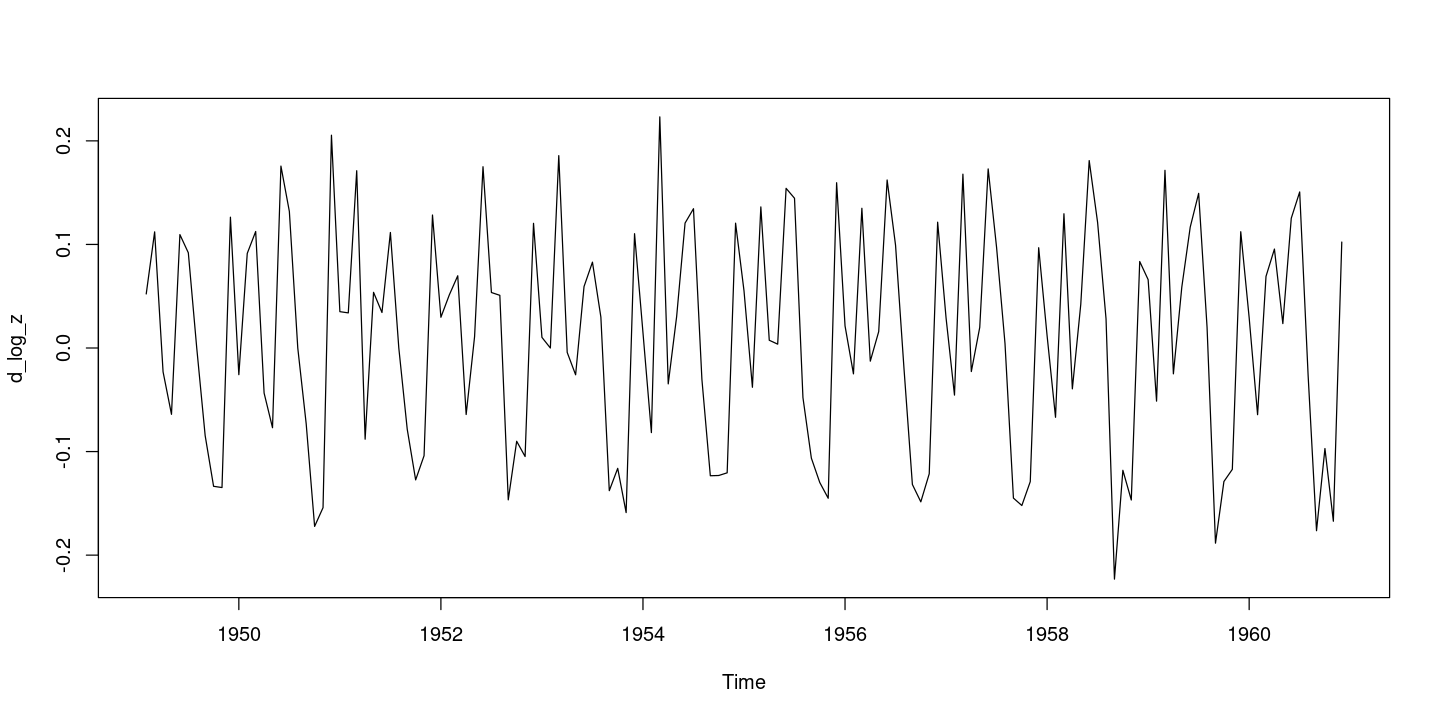
= diff (logz)plot.ts (d_log_z)
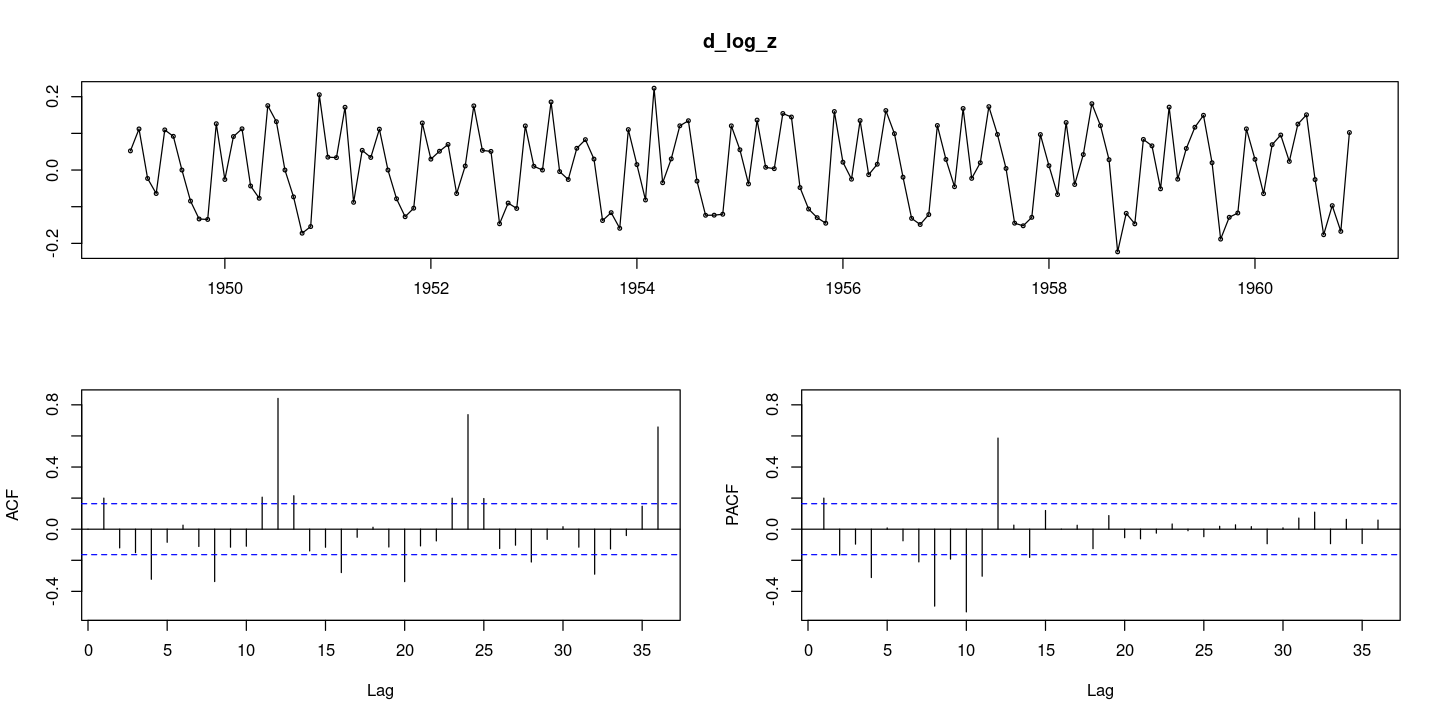
:: tsdisplay (d_log_z, lag.max= 36 )
여전히 계절성분이 남아있으므로, 계절차분 진행
\(Δ_{12}ΔZ_t = (1 − B^{12})(1 − B)Z_t = (1 − B^{12})(Z_t − Z_{t−1}) = Z_t − Z_{t−1} − Z_{t−12} − Z_{t−1}\)
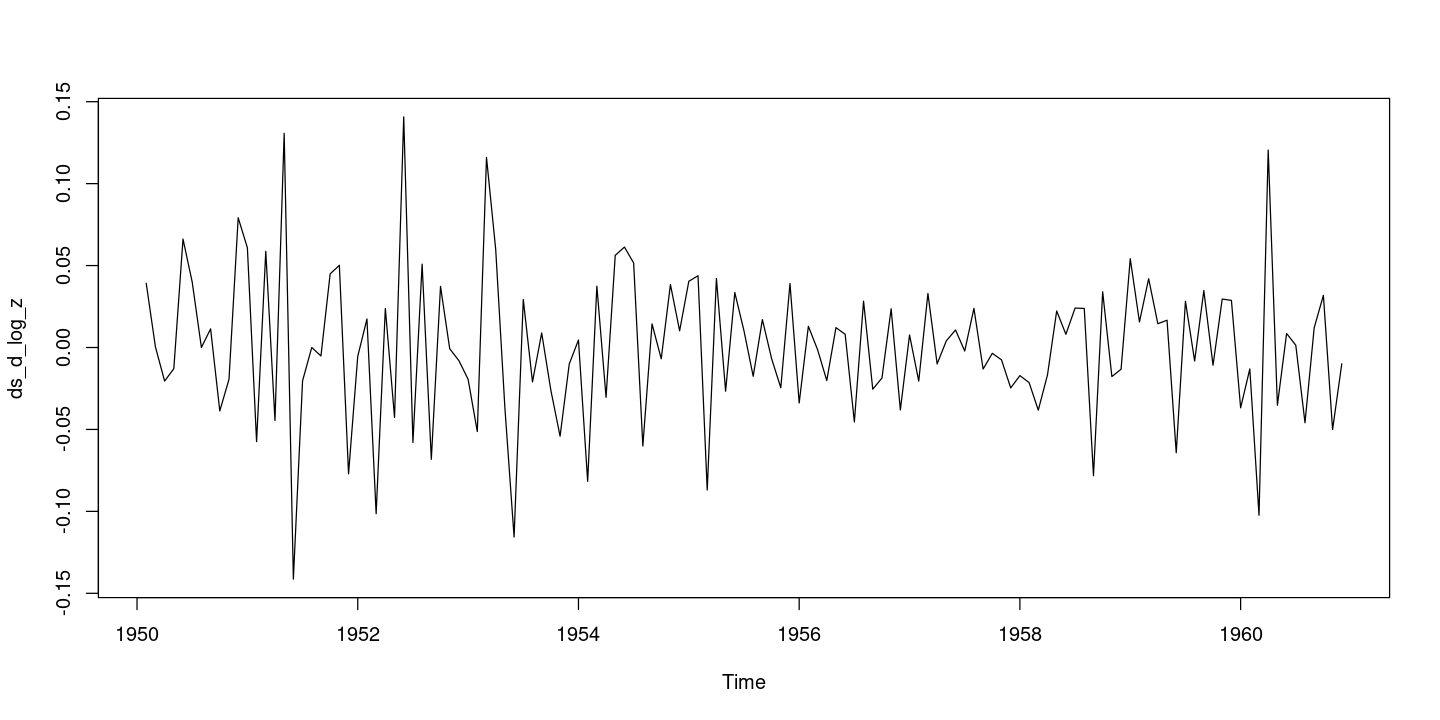
<- diff (d_log_z, 12 )plot.ts (ds_d_log_z)
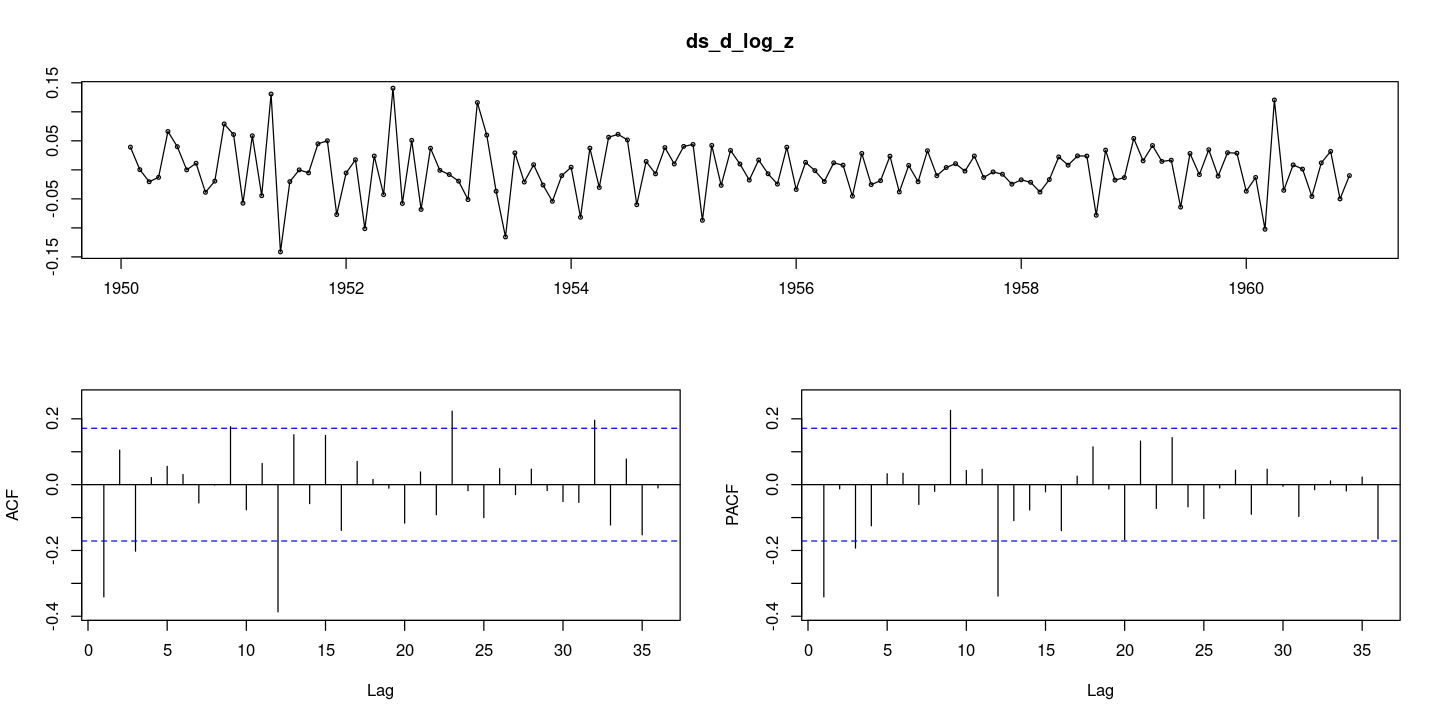
:: tsdisplay (ds_d_log_z, lag.max= 36 )
하지만, 일반적으로 계절성분과 추세가 동시에 있는 경우 계절차분을 먼저 진행한다
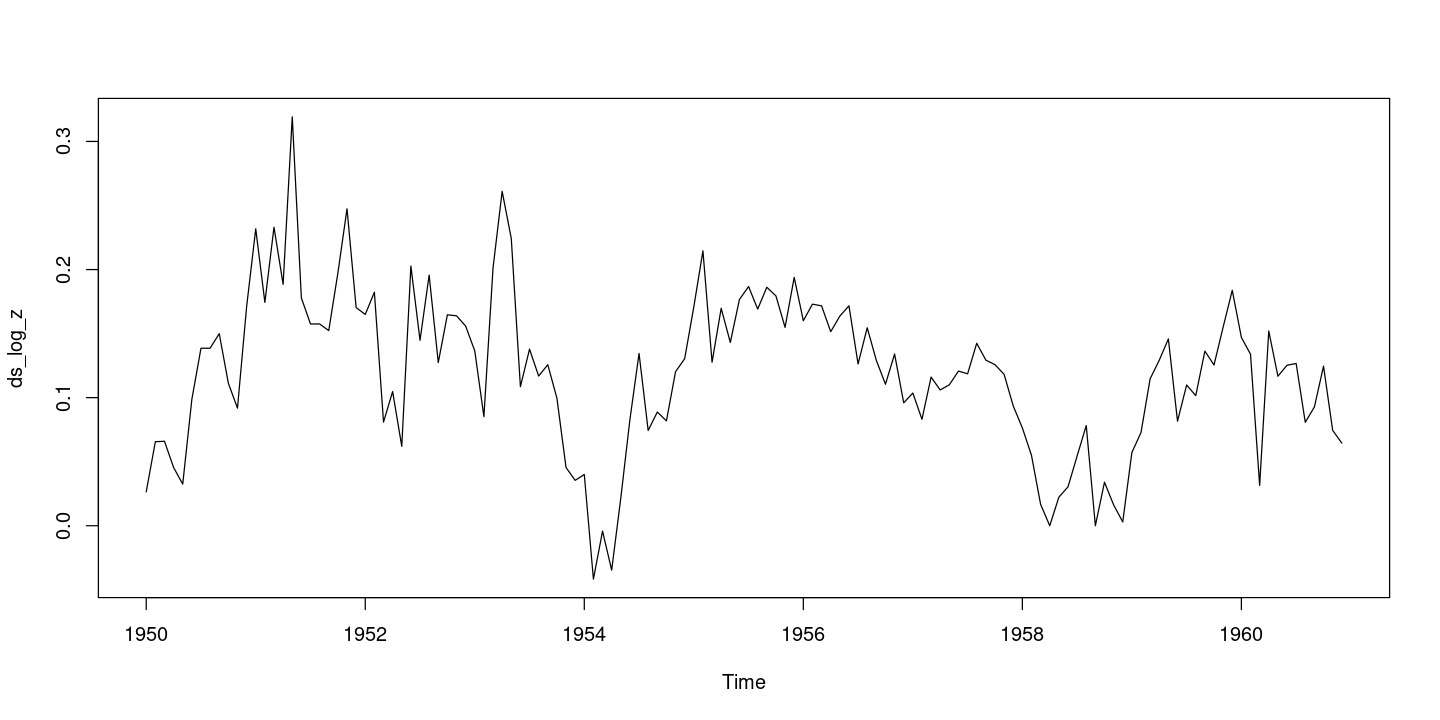
<- diff (logz, 12 )ts.plot (ds_log_z)
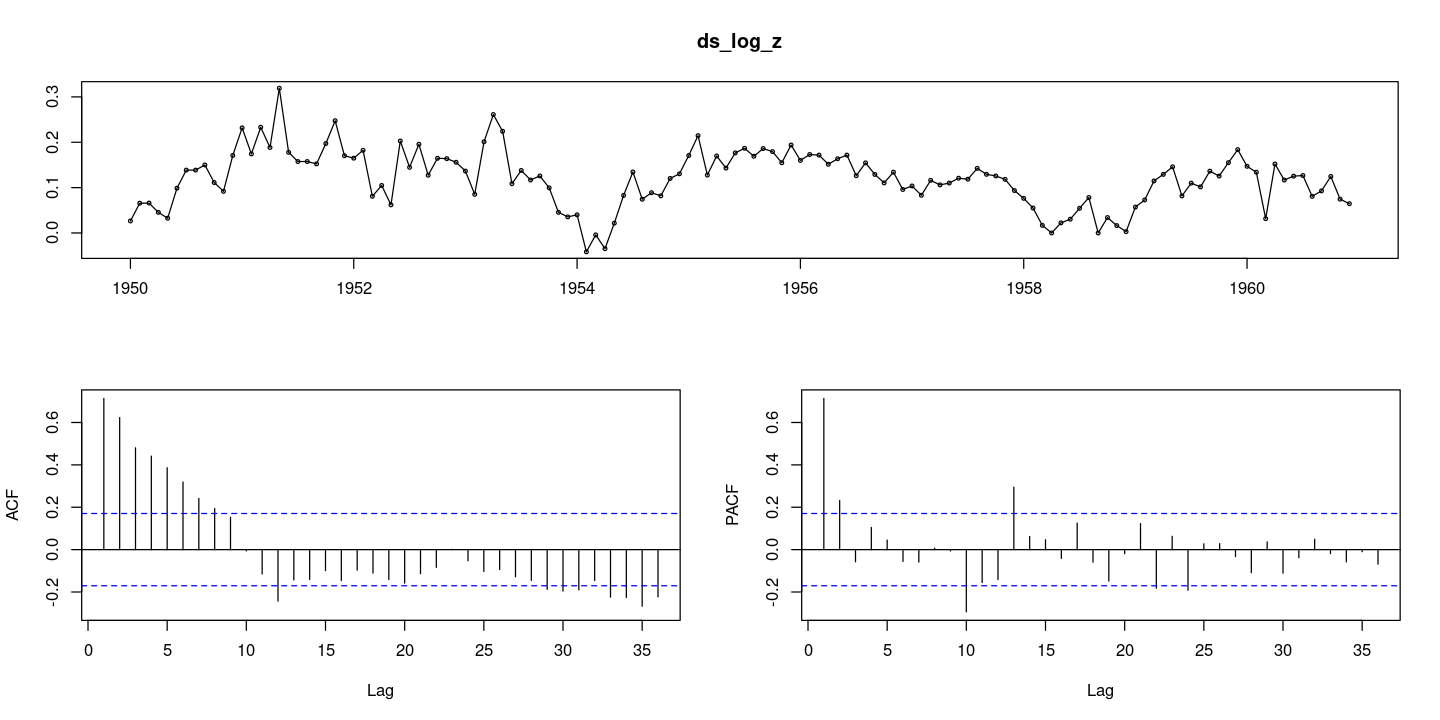
:: tsdisplay (ds_log_z, lag.max= 36 )
확률적추세가 있어 보이지만, AR 모형에서 ACF가 감소하는 형태라고 할 수도 있다. 이 경우에는 추세를 제거하기 위한 차분을 더 진행하는 것을 결정하는 것이 어렵다.
depart data
<- scan ("depart.txt" )plot.ts (z)
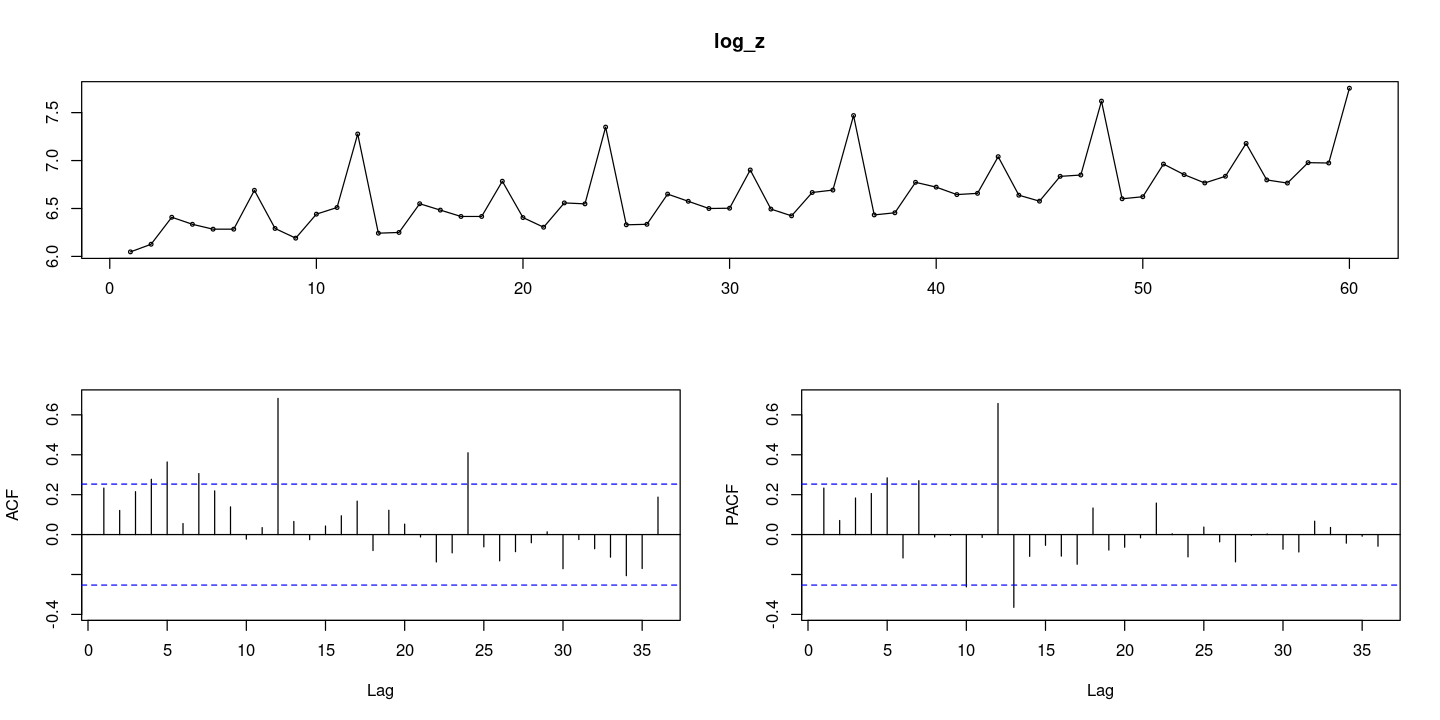
<- log (z):: tsdisplay (log_z, lag.max= 36 )
계절차분을 먼저 진행
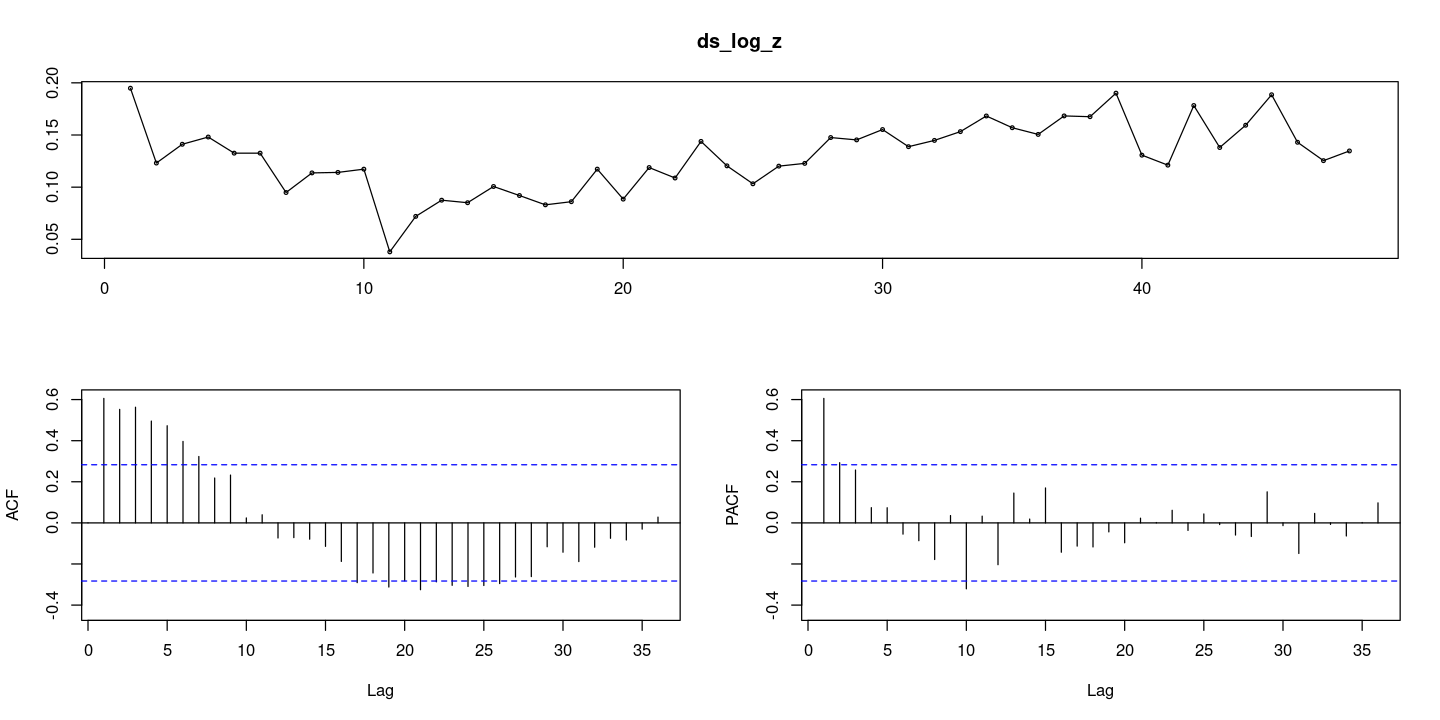
<- diff (log_z, 12 ):: tsdisplay (ds_log_z, lag.max= 36 )
이 데이터 시도표 상으로는 확률적인 추세가 있어보이지만, 역시 ACF만 보고 차분이 필 요한 가에 대한 결정을 하는 것이 쉽지 않다.
여러가지 Simulation
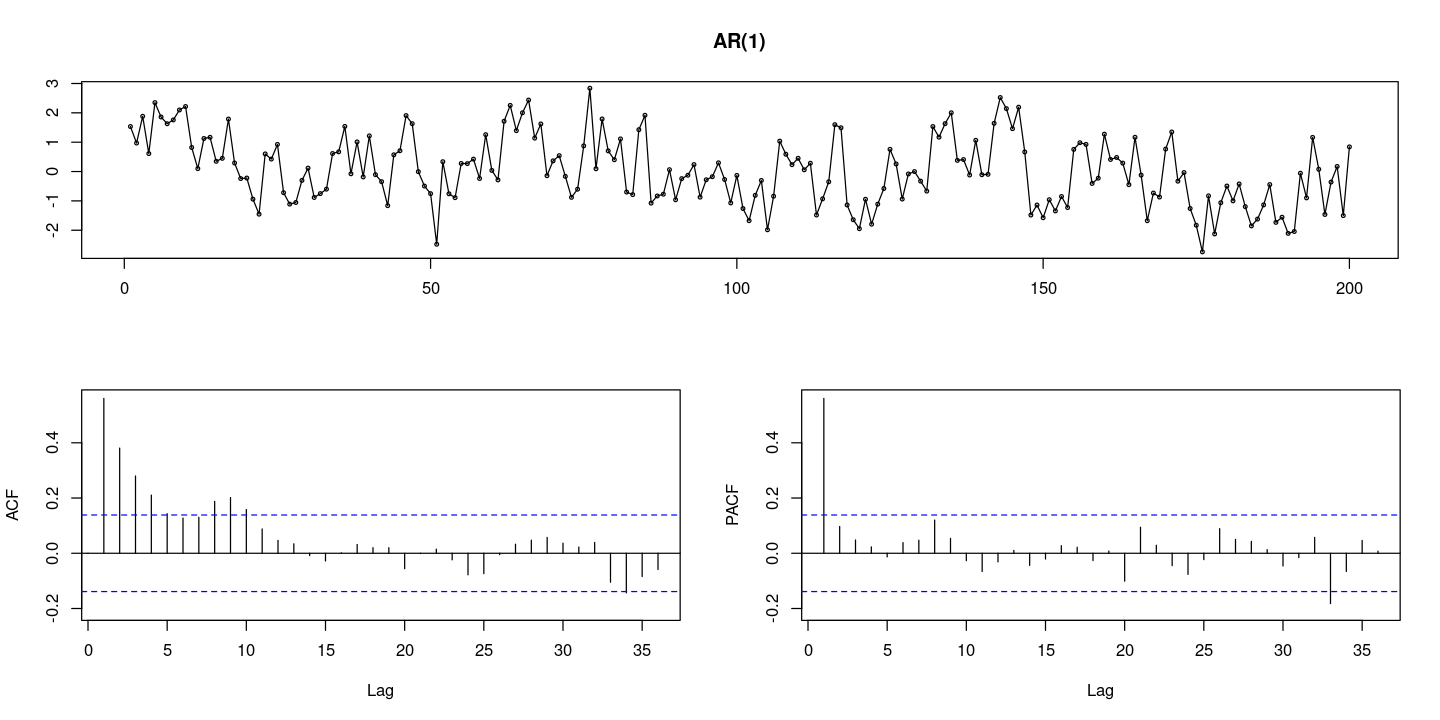
<- 200 = arima.sim (n= n, list (order= c (1 ,0 ,0 ), ar= 0.5 )) #AR(1) = arima.sim (n= n, list (order= c (1 ,1 ,0 ), ar= 0.5 )) #ARIMA(1,1,0)
:: tsdisplay (x, lag.max= 36 , main = "AR(1)" )
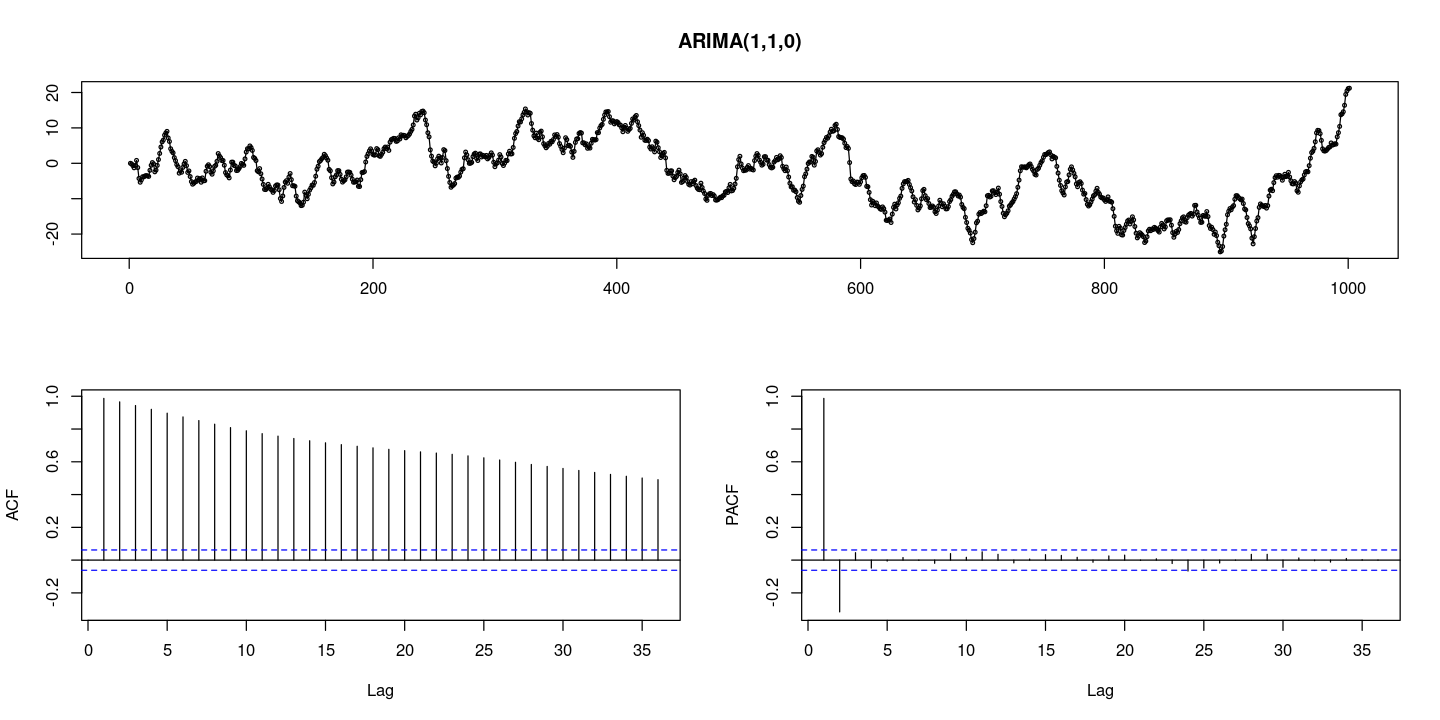
:: tsdisplay (z, lag.max= 36 , main = "ARIMA(1,1,0)" )
acf가 지수적으로 감소하고 있다. 차분이 필요하다.
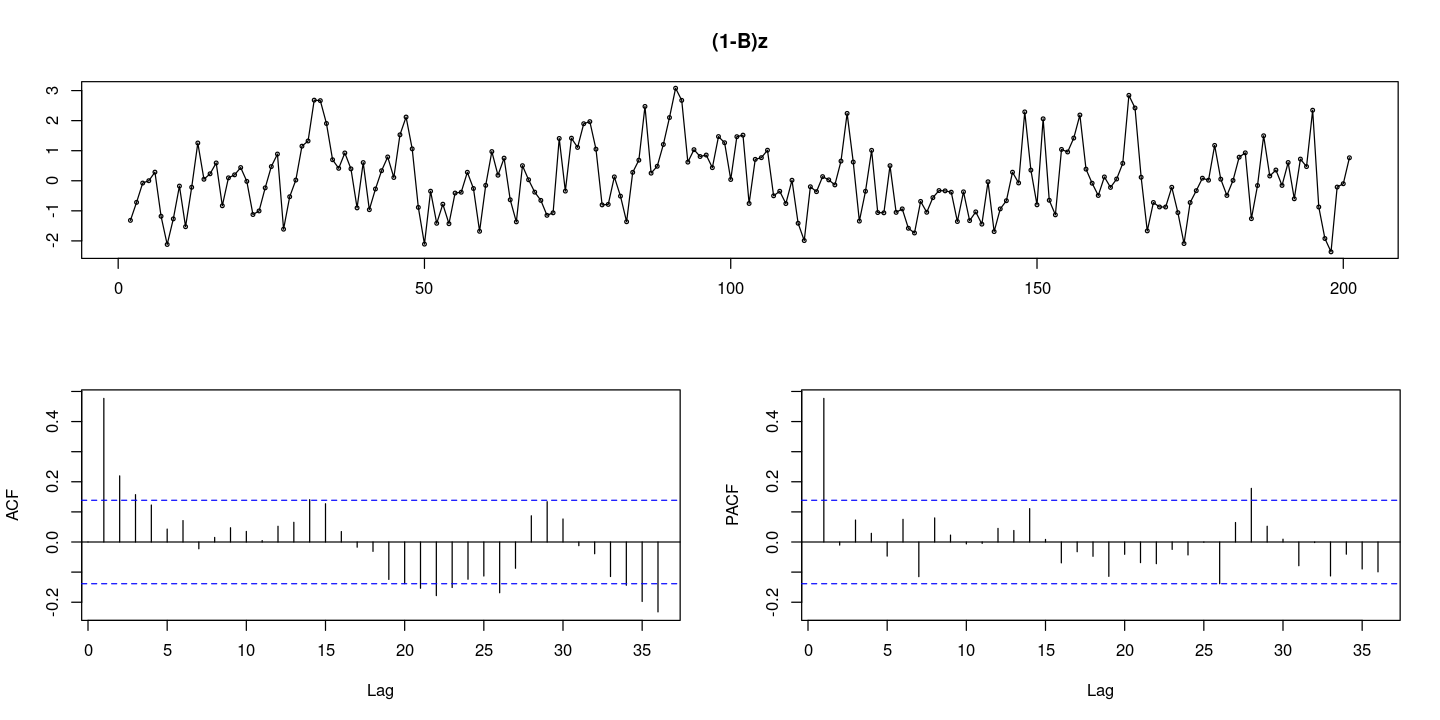
ARIMA(1,1,0)모형은 차분하면 AR(1)모형이 된다.
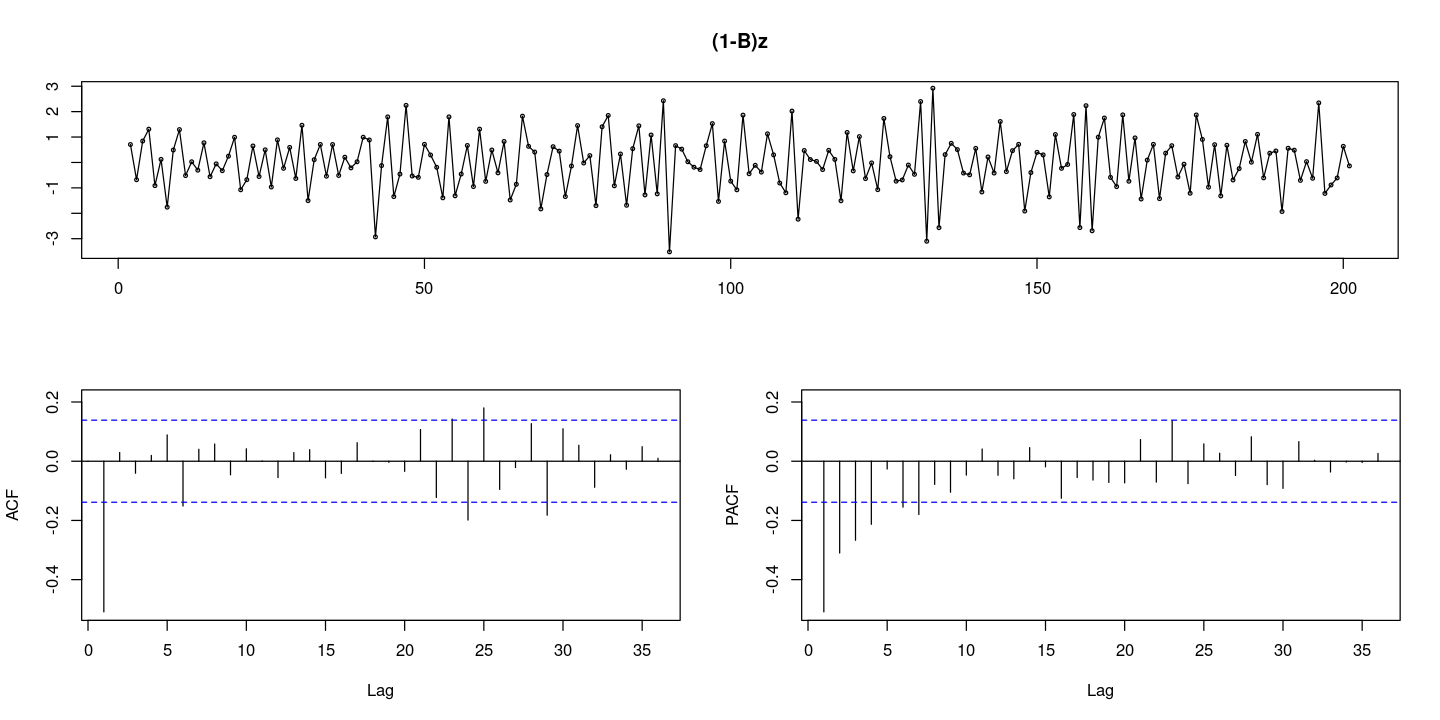
:: tsdisplay (diff (z), lag.max= 36 , main = "(1-B)z" )
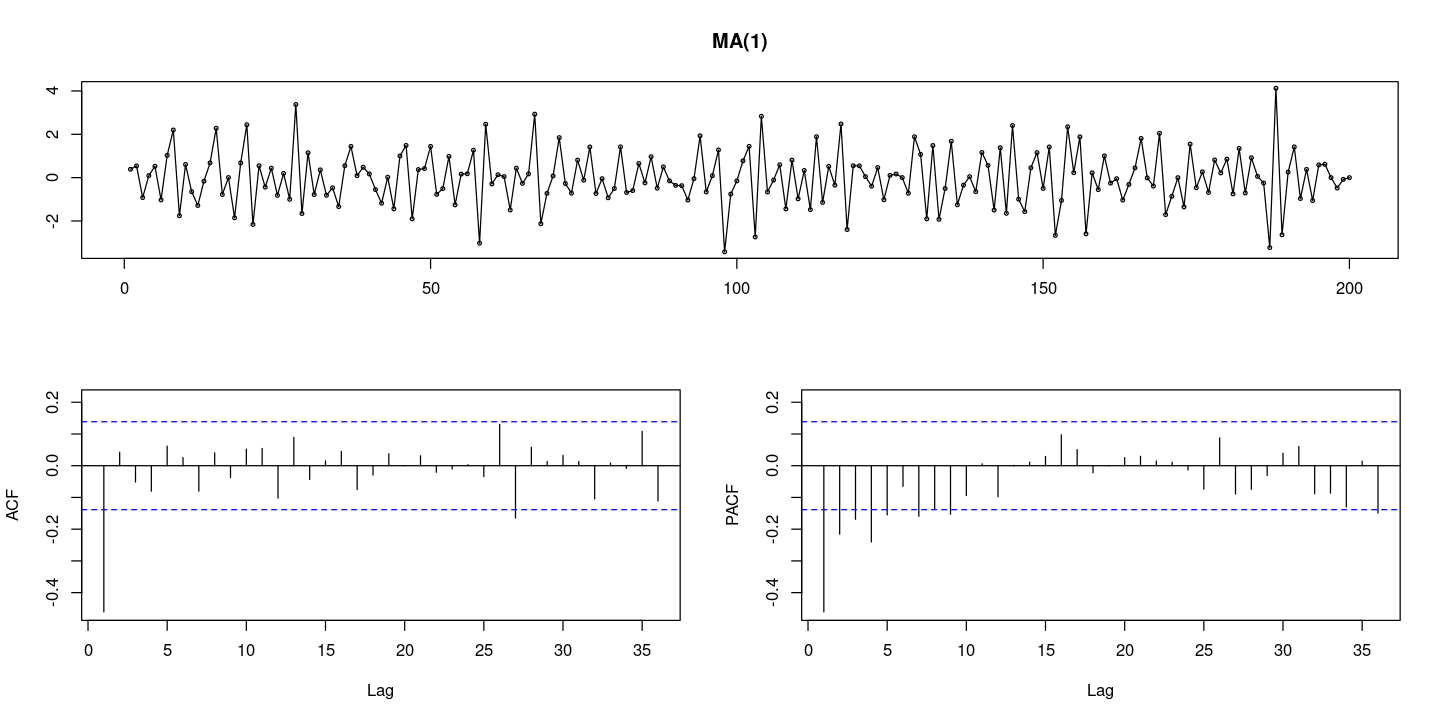
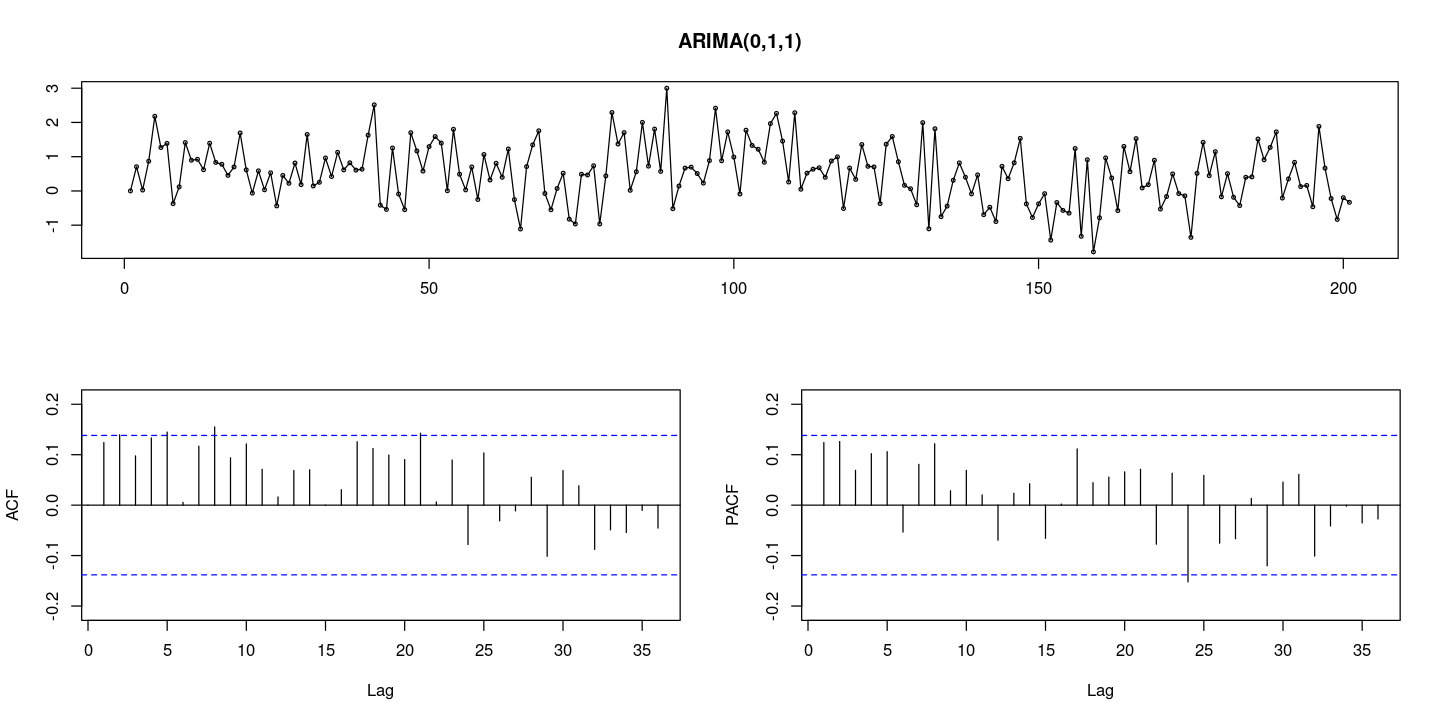
<- 200 = arima.sim (n= n, list (order= c (0 ,0 ,1 ), ma= - 0.8 )) #MA(1) = arima.sim (n= n, list (order= c (0 ,1 ,1 ), ma= - 0.8 )) #ARIMA(0,1,1)
:: tsdisplay (x, lag.max= 36 , main = "MA(1)" )
:: tsdisplay (z, lag.max= 36 , main = "ARIMA(0,1,1)" )
:: tsdisplay (diff (z), lag.max= 36 , main = "(1-B)z" )
<- 200 = arima.sim (n= n, list (order= c (1 ,0 ,1 ), ar= 0.5 , ma= - 0.8 )) #ARMA(1,1) = arima.sim (n= n, list (order= c (1 ,1 ,1 ), ar= 0.5 , ma= - 0.8 )) #ARIMA(1,1,1)
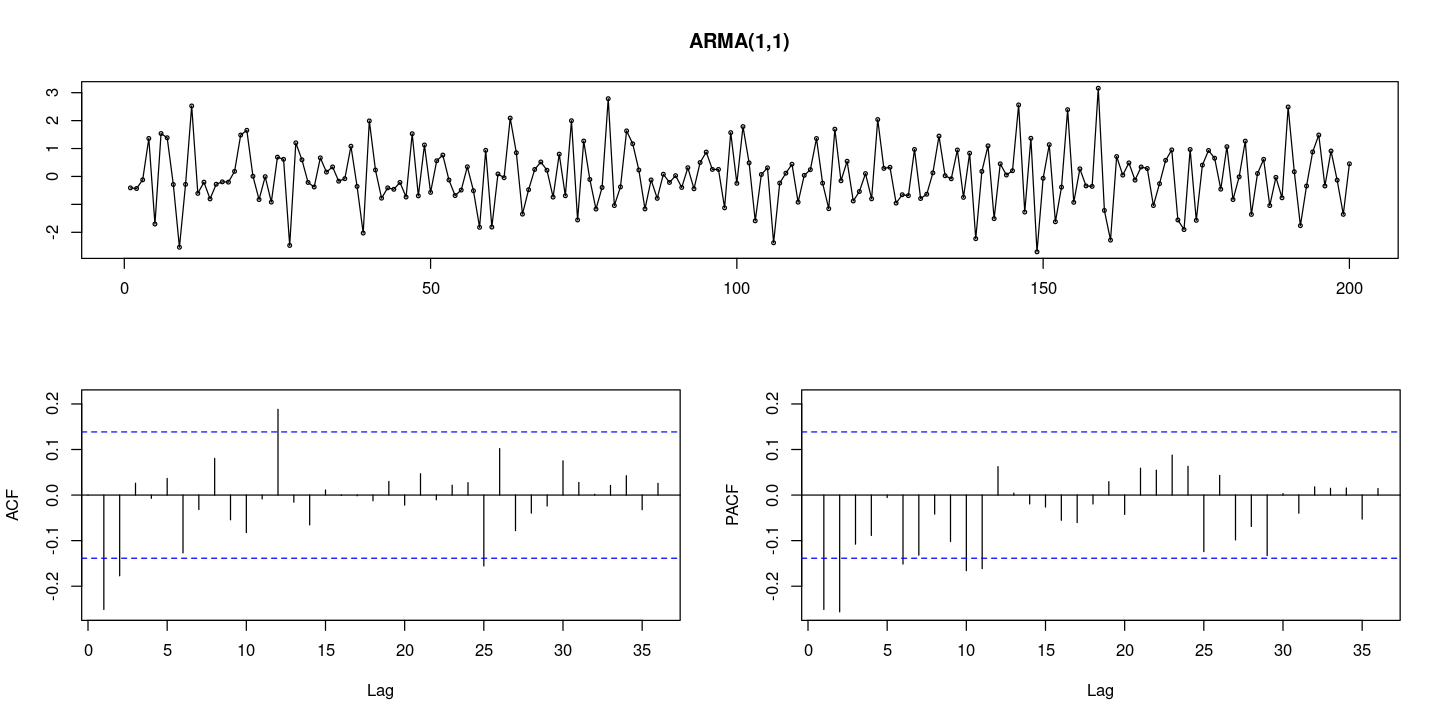
:: tsdisplay (x, lag.max= 36 , main = "ARMA(1,1)" )
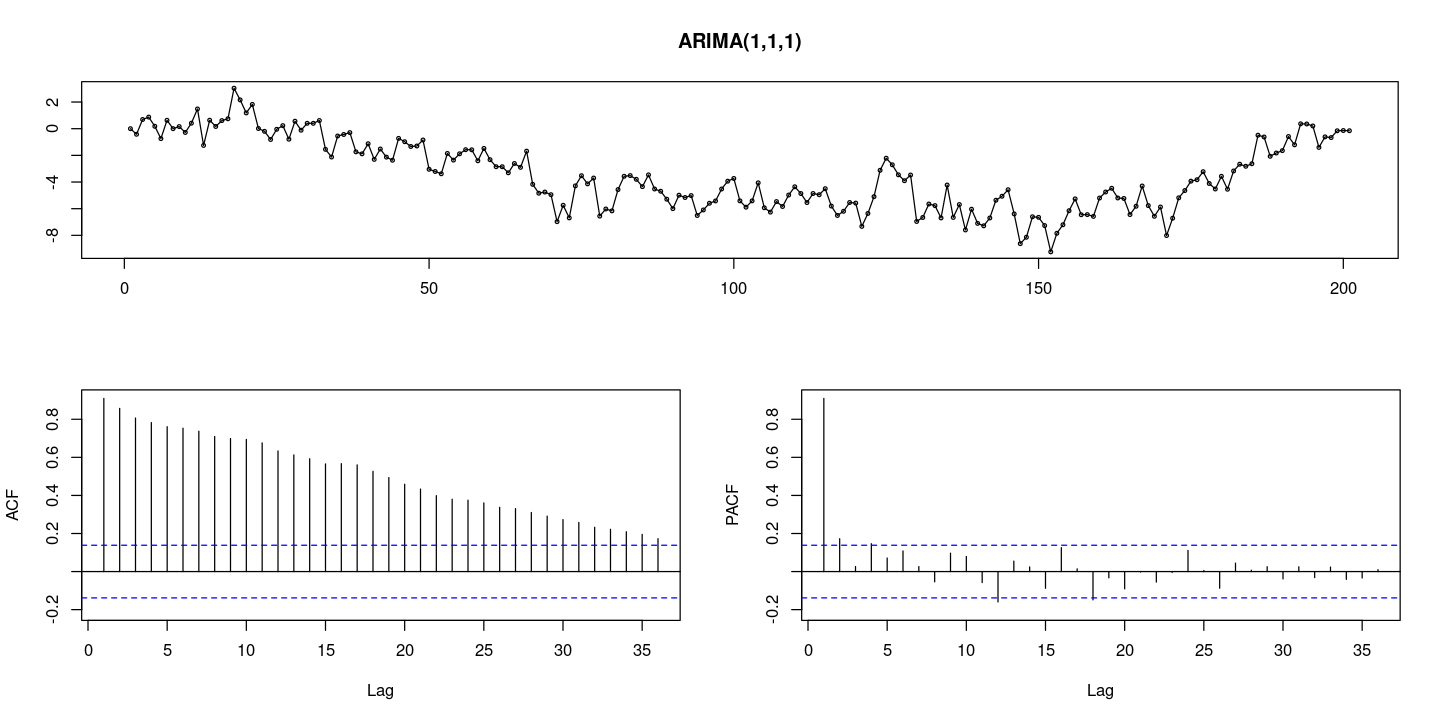
:: tsdisplay (z, lag.max= 36 , main = "ARIMA(1,1,1)" )
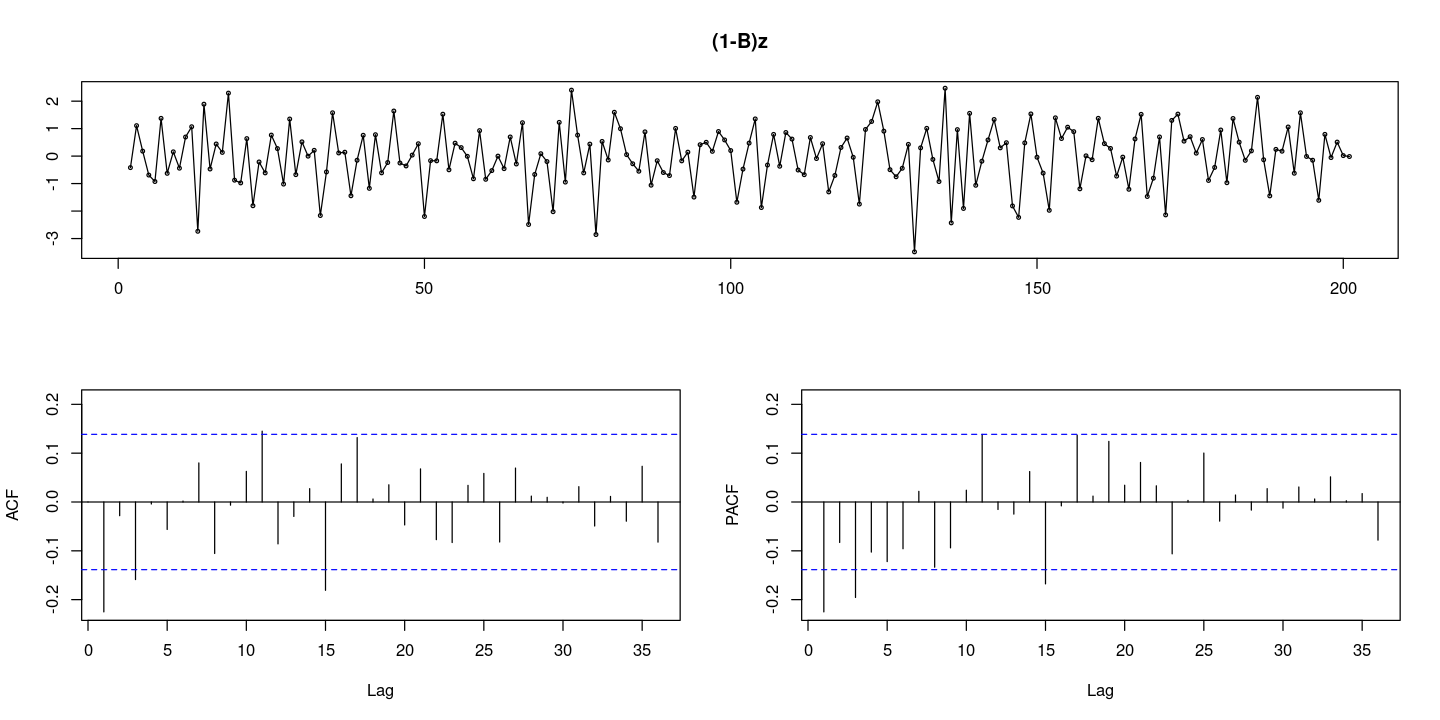
:: tsdisplay (diff (z), lag.max= 36 , main = "(1-B)z" )
과대차분
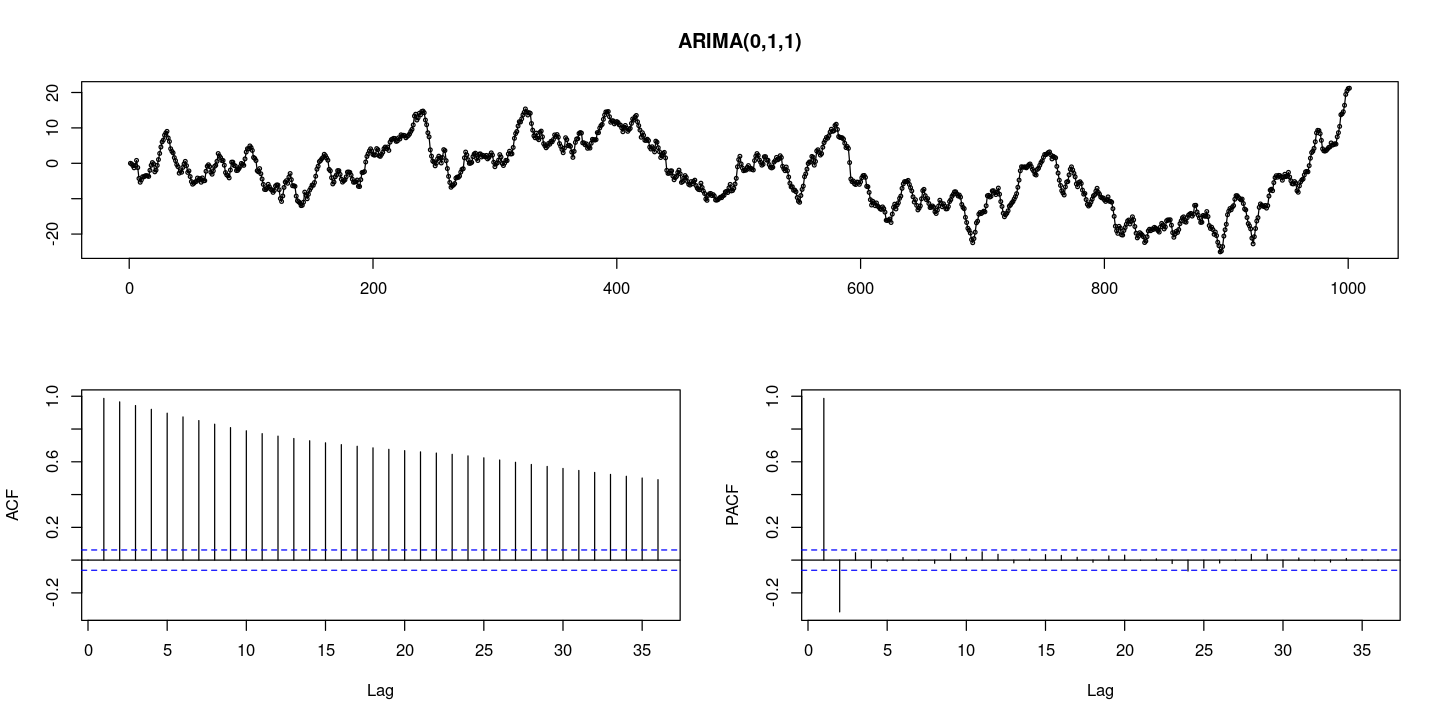
## ARIMA(0,1,1) = arima.sim (n= 1000 , list (order= c (0 ,1 ,1 ), ma= 0.5 ))
:: tsdisplay (z, lag.max= 36 , main = "ARIMA(0,1,1)" )
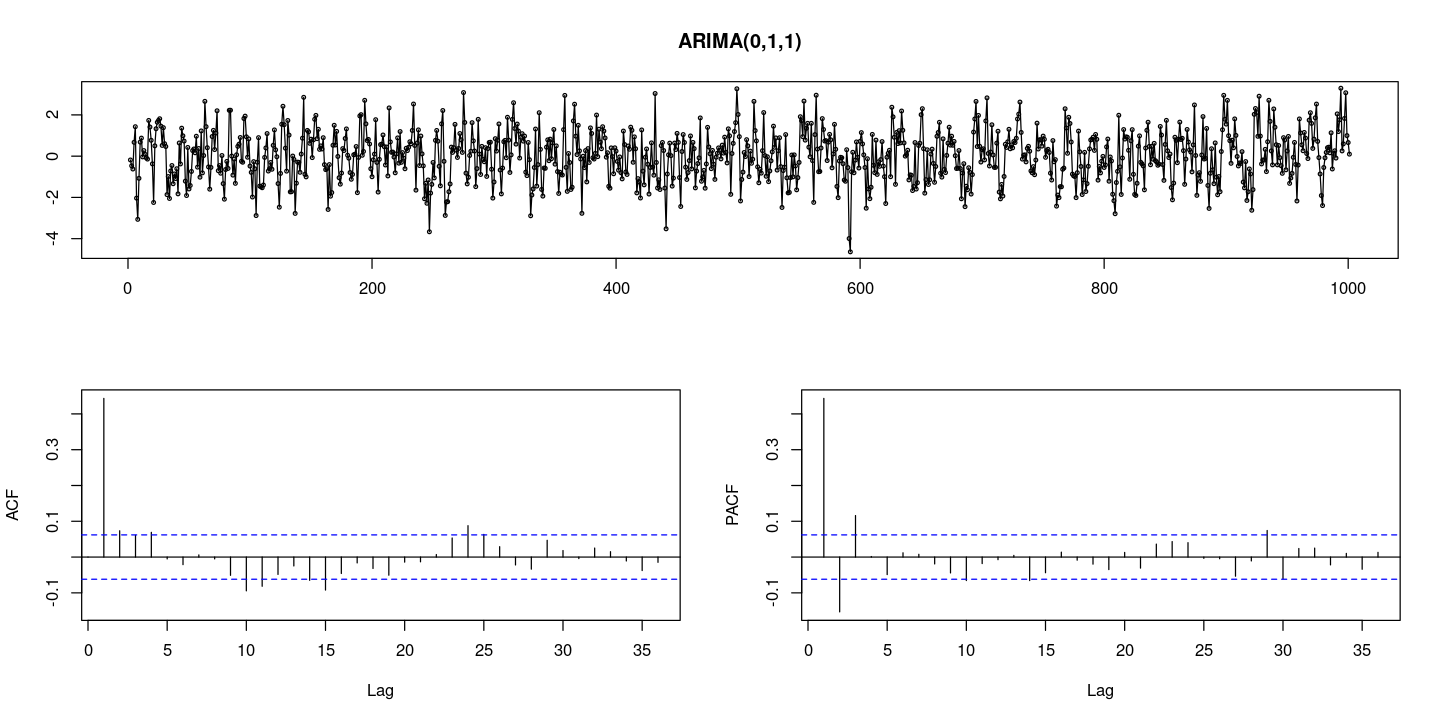
#한 번 차분 <- diff (z):: tsdisplay (d_z, lag.max= 36 , main = "ARIMA(0,1,1)" )
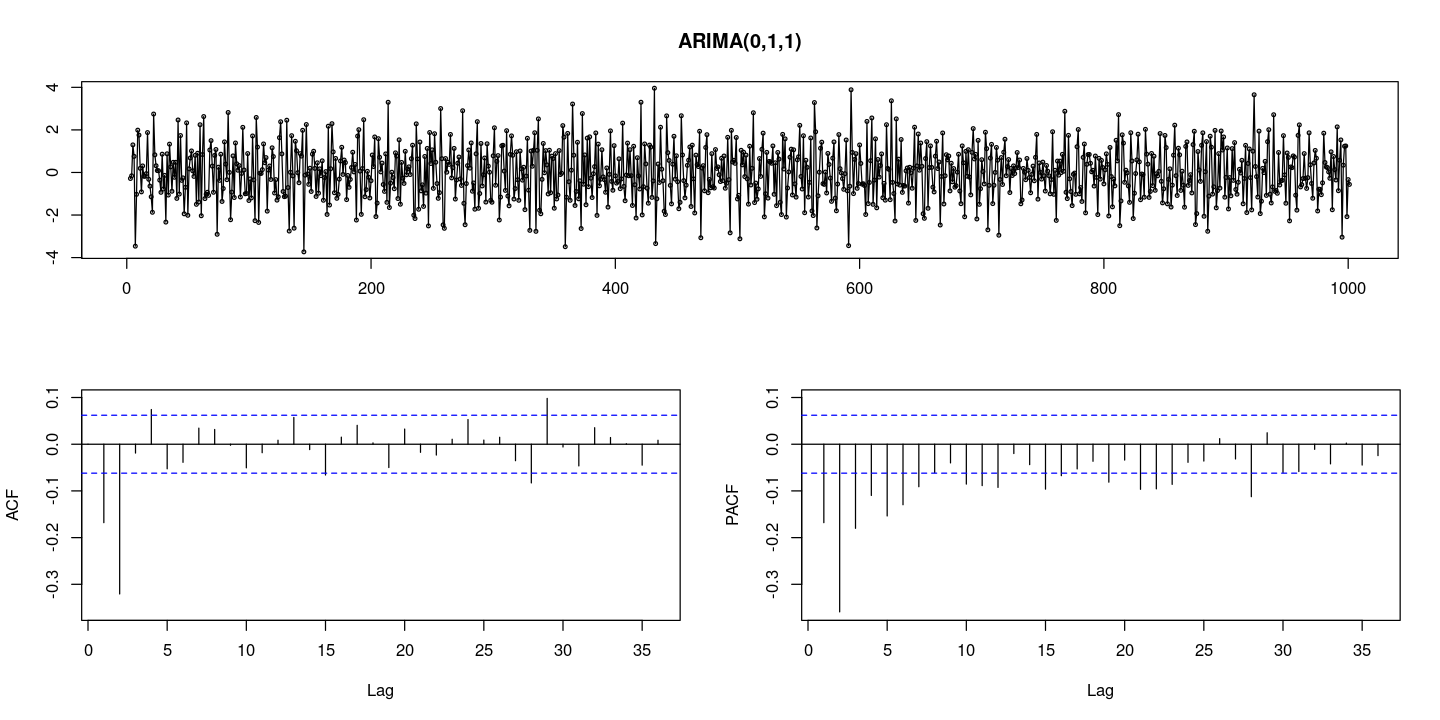
# 한 번 더 차분 <- diff (d_z):: tsdisplay (d2_z, lag.max= 36 , main = "ARIMA(0,1,1)" )
한 번 차분을 하면 정상시계열이 된다. 그리고 한 번 더 차분해도 마찬가지로 정상시계 열이다
sd (z)sd (diff (z))sd (diff (diff (z)))
8.72895467185367
1.18251197758341
1.2484612507557
차분을 두번 하고 나면 분산이 커진다. 이를 과대차분이라고 한다